
Faisons le point :
Nous pouvons voir que l'intérêt majeur du système de numération à base 16 ou hexadécimal, est le fait qu'il nous permet de représenter visuellement le contenu d'une mémoire d'ordinateur en évitant l'obligation d'aligner d'interminables séries de 1 et de 0 du système binaire.
Bien entendu, voir une telle "photocopie" de mémoire ne nous apprendra pas grand'chose pour l'instant car encore faut-il savoir où une information commence, et où elle finit. Car en effet, un octet peut représenter une donnée, une partie de donnée ou encore une instruction ou partie d'instruction d'un programme. Pour clarifier tout ça une approche de notions de programmation et de langage machine sera indispensable.
Petit souvenir
personnel : A l'époque de mes débuts en informatique, les calculettes hexa n'étaient
pas courantes. Ainsi le seul outil de conversion dont nous disposions,
offert gracieusement par les constructeurs d'ordinateurs, consistait en
un petit dépliant comportant la table de conversion ci-dessous :
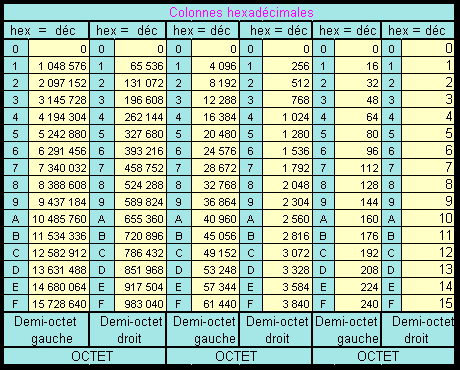
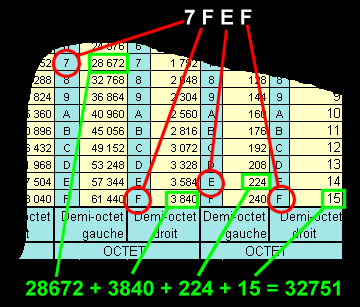
Mode d'emploi de la table : exemple convertir l'hexa 7FEF en décimal
Bien entendu l'inverse est également possible : Convertir 32751 en Hexa. On procède comme suit :
On cherche dans la table le nombre décimal égal ou immédiatement inférieur à 32751. On trouve 28672 ou hexa 7 en col.4
On fait la différence entre 32751 et 28672 = 4079
On cherche dans la table le nombre décimal égal ou immédiatement inférieur à 4079. On trouve 3840 ou hexa F en col.3
On fait la différence entre 4079 et 3840 = 239
On cherche dans la table le nombre décimal égal ou immédiatement inférieur à 239. On trouve 224 ou hexa E en col.2
On fait la différence entre 239 et 224 = 15
On cherche dans la table le nombre décimal égal à 15. On trouve 15 ou hexa F en col.1
Résultat : 7FEF cqfd
